- Joined
- Jul 9, 2014
- Messages
- 6,171
- Reaction score
- 8,157
The canonical quantization you're taught - replace {f,g} with [f, g]/iℏ - is, well, ill-defined. You can always add a classical 0 that becomes non-zero quantumly (thanks, non-commutation). But there's another way: geometric quantization.
It all starts with symplectic geometry. Think of a classical phase space, but forget coordinates for the moment. What you require is something called a symplectic form - a closed, non-degenerate 2-form, ω.
Now, if ω is "integral" (its cohomology class is integral), then you can construct a line bundle L over your phase space, with a connection ▽ whose curvature is -iω.
This, friends, is the so-called "prequantum line bundle."
But we're not quantizing yet. We require a
"polarization" — some clever way to slice up phase space into "position" and "momentum" subspaces (technically, a Lagrangian foliation). This is where the Kähler manifolds come in. They give this polarization.
Sections of L that are covariantly constant along your polarization form a vector space. If you've chosen a Kahler polarization, this space gets a natural inner product. Cool. Now you've got a Hilbert space, from pure geometry.
Classical observables (functions on phase space) can be "lifted" to operators on this Hilbert space. The problem is that this lift isn't unique. You need a "metaplectic correction" (a story for another time) to get it "just right.”
Geometric quantization is beautiful, and more sherdoggers should know this framework.
It even tells us that only certain classical states (Bohr-Sommerfeld leaves) have quantum counterparts.
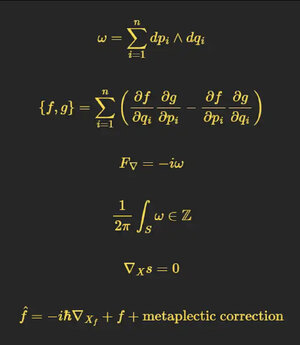
It all starts with symplectic geometry. Think of a classical phase space, but forget coordinates for the moment. What you require is something called a symplectic form - a closed, non-degenerate 2-form, ω.
Now, if ω is "integral" (its cohomology class is integral), then you can construct a line bundle L over your phase space, with a connection ▽ whose curvature is -iω.
This, friends, is the so-called "prequantum line bundle."
But we're not quantizing yet. We require a
"polarization" — some clever way to slice up phase space into "position" and "momentum" subspaces (technically, a Lagrangian foliation). This is where the Kähler manifolds come in. They give this polarization.
Sections of L that are covariantly constant along your polarization form a vector space. If you've chosen a Kahler polarization, this space gets a natural inner product. Cool. Now you've got a Hilbert space, from pure geometry.
Classical observables (functions on phase space) can be "lifted" to operators on this Hilbert space. The problem is that this lift isn't unique. You need a "metaplectic correction" (a story for another time) to get it "just right.”
Geometric quantization is beautiful, and more sherdoggers should know this framework.
It even tells us that only certain classical states (Bohr-Sommerfeld leaves) have quantum counterparts.
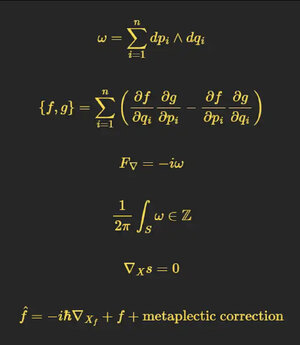
Last edited:
